Equazione di Bellman e Intelligenza Artificiale
L'equazione di Bellman è una delle fondamenta della teoria del controllo ottimale e della programmazione dinamica. Introdotta da Richard Bellman negli anni '50, questa equazione fornisce un approccio sistematico per risolvere problemi di decisione sequenziali, che sono prevalenti in vari campi come l'ingegneria, l'economia, la biologia e, più recentemente, l'intelligenza artificiale (IA).

Che cos'è l'Equazione di Bellman?
Richard Bellman, matematico e pioniere della teoria del controllo ottimale, sviluppò l'equazione che porta il suo nome durante il suo lavoro alla RAND Corporation negli anni '50. Bellman stava cercando un metodo per risolvere problemi complessi di decisione in cui le scelte attuali influenzano non solo i risultati immediati ma anche quelli futuri. La sua intuizione fu di dividere un problema di decisione a lungo termine in una serie di decisioni più semplici e successive, un approccio che chiamò "programmazione dinamica". Bellman formulò il problema come una funzione di valore che esprime il valore ottimale atteso a partire da uno stato iniziale, considerando tutte le possibili scelte future. L'equazione di Bellman cattura questa idea e permette di trovare la soluzione ottimale mediante un processo iterativo. L'equazione di Bellman può essere espressa in modo generale come:
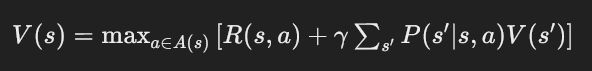
Vediamo passo per passo cosa significa ciascun termine:
- V(s)V(s): questa è la funzione di valore stato, che rappresenta il valore atteso massimo dell'essere nello stato ss. In altre parole, è la somma delle ricompense che ci si aspetta di ottenere in futuro a partire dallo stato ss e seguendo la politica ottimale.
- maxa∈A(s)maxa∈A(s): questo indica che vogliamo trovare l'azione aa tra tutte le azioni possibili A(s)A(s) nello stato ss che massimizza il valore. È il principio dell'ottimizzazione.
- R(s,a)R(s,a): questa è la ricompensa immediata ricevuta dopo aver preso l'azione aa nello stato ss. È un valore numerico che rappresenta il beneficio immediato di quell'azione.
- γγ: questo è il fattore di sconto, un valore compreso tra 0 e 1. Indica quanto le ricompense future sono importanti rispetto a quelle immediate. Un valore di γγ vicino a 1 significa che le ricompense future sono quasi importanti quanto quelle immediate, mentre un valore vicino a 0 significa che si dà più peso alle ricompense immediate.
- ∑s′P(s′∣s,a)V(s′)∑s′P(s′∣s,a)V(s′): questa è la somma delle funzioni di valore degli stati successivi s′s′, ponderata dalla probabilità di transizione P(s′∣s,a)P(s′∣s,a). P(s′∣s,a)P(s′∣s,a) rappresenta la probabilità di finire nello stato s′s′ dopo aver preso l'azione aa nello stato ss.
L'equazione di Bellman è uno strumento potente per risolvere problemi di decisione sequenziale, scomponendo il problema in decisioni più piccole e iterative. Questa equazione è alla base di molti algoritmi di apprendimento per rinforzo, consentendo agli agenti di apprendere politiche ottimali attraverso l'interazione con l'ambiente. L'equazione di Bellman può essere formulata per un processo decisionale Markoviano (MDP), che è un modello matematico per prendere decisioni in situazioni dove gli esiti sono in parte casuali e in parte sotto il controllo di un decisore.
Equazione di Bellman ed Intelligenza Artificiale
L'apprendimento per rinforzo (RL) è una branca dell'IA che si focalizza su come gli agenti dovrebbero agire in un ambiente per massimizzare una ricompensa cumulativa. L'equazione di Bellman è fondamentale per molti algoritmi di RL, tra cui Q-Learning e Deep Q-Networks (DQN). Applicazioni dell'Equazione di Bellman nell'Intelligenza Artificiale
L'equazione di Bellman e gli algoritmi di RL basati su di essa hanno rivoluzionato molti campi applicativi dell'IA, tra cui:
- Giochi: gli algoritmi di RL sono stati utilizzati per sviluppare agenti in grado di giocare a giochi complessi come Atari, Go e scacchi. Ad esempio, DeepMind ha sviluppato agenti che superano le prestazioni umane in molti giochi Atari utilizzando DQN.
- Robotica: gli algoritmi di RL permettono ai robot di apprendere comportamenti complessi, come la locomozione e la manipolazione di oggetti. Questi algoritmi consentono ai robot di adattarsi a diversi ambienti e compiti in modo autonomo.
- Finanza: l'apprendimento per rinforzo viene utilizzato per sviluppare strategie di trading algoritmico che possono adattarsi dinamicamente alle condizioni di mercato variabili, migliorando la gestione del rischio e l'ottimizzazione dei profitti.
- Healthcare: gli algoritmi di RL vengono impiegati per ottimizzare i trattamenti medici personalizzati, migliorare la gestione delle risorse ospedaliere e sviluppare protocolli di trattamento basati su dati storici e in tempo reale.
Conclusione
L'equazione di Bellman è un pilastro della teoria del controllo ottimale e della programmazione dinamica, fornendo una base solida per lo sviluppo di algoritmi di
apprendimento per rinforzo nell'intelligenza artificiale. La capacità di questa equazione di decomporre problemi complessi in decisioni sequenziali più semplici ha permesso significativi avanzamenti tecnologici e applicativi in vari settori. Con il continuo sviluppo delle tecniche di RL e l'integrazione con il
deep learning, l'equazione di Bellman continuerà a giocare un ruolo cruciale nel futuro dell'IA
Dott.Igor Graziato
Psicologo del Lavoro e delle organizzazioni
Specialista in Psicoterapia
Virtual Reality Therapist
Master in Cognitive Behavioural Hypnotherapy
Ipnosi Clinica Evidence Based
Membro dell'American Psychological Association
Past Vice President Ordine degli Psicologi del Piemonte
Desideri maggiori informazioni?
Inviando una richiesta si dichiara di aver letto il disclaimer sulla privacy e si autorizza lo studio RPStrategy© ad elaborare una risposta.
